Congettura di Collatz – un metodo grafico per svolgere il suo algoritmo
In appendice un teorema per mostrare la limitatezza dei tratti di crescita nell’algoritmo legato alla Congettura di Collatz
di Oreste Caroppo
Abstract
Proporremo qui un metodo grafico per lo svolgimento dell’algoritmo che è alla base della famosa Congettura di Collatz.
Premessa
La Congettura non ancora dimostrata nella sua verità o falsità riguarda il seguente algoritmo:
si prenda un intero positivo n
ora se n = 1, l’algoritmo termina
in caso contrario n può essere o pari, o dispari e diverso da 1
se n è pari, si divide n per due
altrimenti se n è dispari diverso da 1, si moltiplica n per 3 e si aggiunge 1.
A questo punto si riparte in loop con l’algoritmo utilizzando il nuovo numero intero ottenuto come nuovo valore di n.
La Congettura di Collatz asserisce che questo algoritmo giunge sempre a termine, indipendentemente dal valore di partenza, pertanto in un numero finito di cicli.
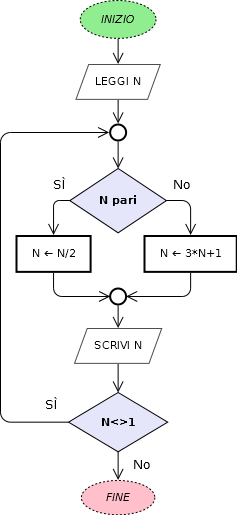
Vediamo nell’immagine di seguito un diagramma di flusso (flow chart) per il semplicissimo algoritmo della Congettura di Collatz:
La ricerca di un metodo grafico
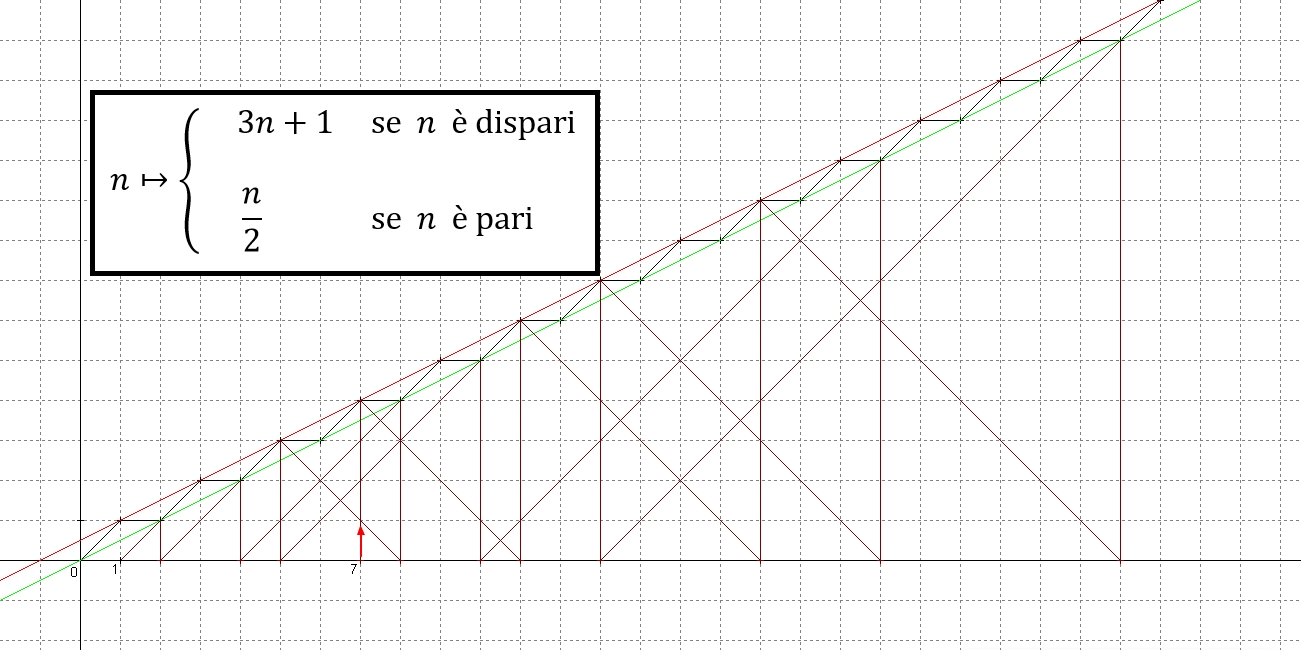
Ora possiamo osservare che quando n dispari 3n+1 sarà sempre un numero pari quindi un numero su cui l’algoritmo farà sì che si proceda a dividerlo per 2, per cui possiamo riformulare equivalentemente l’algoritmo della Congettura dicendo che “se n è dispari diverso da 1, si moltiplica n per 3 si somma 1 e si divide tutto per due: 3n/2+1/2”
Per tentare di sviluppare una procedura grafica per svolgere l’algoritmo riformuliamo l’algoritmo in questo modo equivalente, sostituendo anche il simbolo x al simbolo parametrico n:
Se x è pari, passiamo al numero: x-x/2
Se x è dispari e diverso da 1, passiamo al numero: x +x/2+1/2
Rispetto a x adesso possiamo dire equivalentemente che nel caso di x pari dobbiamo sottrarre a x la quantità x/2, mentre nel caso di x dispari maggiore di 1 dobbiamo aggiungere la quantità x/2+1/2.
A questo punto passiamo su un piano cartesiano e rappresentiamo le funzioni
y = x/2 che è una retta che indichiamo in verde
y = x/2+1/2 che è una retta che indichiamo in rosso
Per ogni punto pari sull’asse delle ascisse indichiamo il punto corrispondente di pari ascissa sulla retta verde, mentre per ogni punto dispari indichiamo il punto corrispondente di pari ascissa sulla retta rossa. Ora congiungiamo alternativamente da destra a sinistra i punti sulle due rette con dei segmenti neri ottenendo la regolare spezzata nera che vediamo nel grafico.
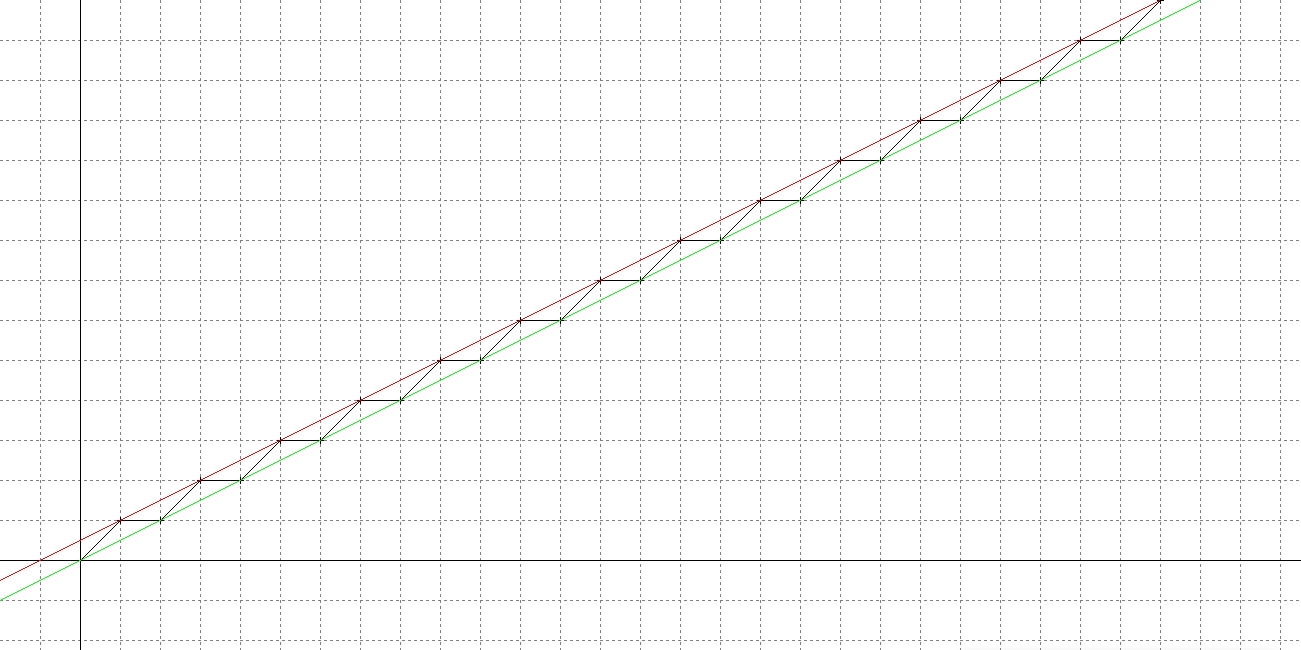
A questo punto è facile capire che partendo da un qualsiasi punto intero positivo n=x maggiore di 1 sull’asse delle ascisse possiamo applicare l’algoritmo procedendo graficamente in questo modo: da tale punto con un segmento verticale si sale fino ad intercettare la spezzata e pertanto fermandosi sulla retta verde se n è pari, sulla retta rossa se n è dispari. Se tale punto della spezzata è una cuspide rivolta verso l’alto, condizione che corrisponde a n dispari, allora ci muoveremo scendendo lungo un segmento inclinato di 45° verso destra (la destra di chi guarda il piano cartesiano) sino ad intercettare l’asse delle ascisse, viceversa se tale punto della spezzata è una cuspide rivolta verso il basso, condizione che corrisponde a n pari, allora ci muoveremo scendendo lungo un segmento sempre inclinato di 45° ma questa volta verso sinistra (la sinistra di chi guarda il piano cartesiano) sino ad intercettare l’asse delle ascisse. Non è difficile dimostrare che tale nuovo punto intercettato in tal modo sull’asse delle ascisse avrà proprio ascissa corrispondente al nuovo numero intero positivo da cui ripartire nell’algoritmo se diverso da 1, e quindi equivalentemente sarà il nuovo punto da cui ripartire (se di ascissa diversa da 1) nel metodo grafico qui esposto. Discendere lungo rette inclinate di 45° gradi nel modo detto equivale se si procede verso destra ad aggiungere ad x l’ordinata del punto corrispondente sulla spezzata, mentre se si procede verso sinistra equivale a sottrarre ad x l’ordinata del punto corrispondente sulla spezzata.
Di seguito vediamo solo un esempio con l’applicazione di questo metodo grafico per l’algoritmo al numero n = 7:
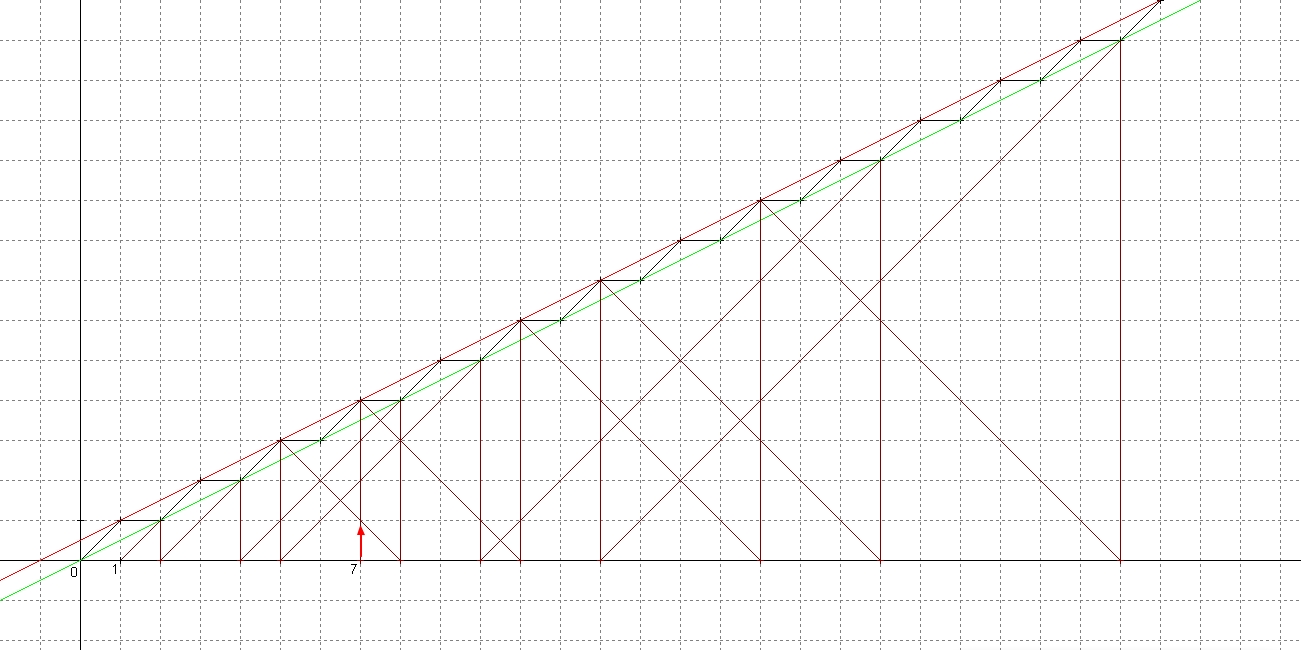
E notiamo come dopo vari passaggi seguendo, a partire dal punto 7 sull’asse delle ascisse, la spezzata del medesimo colore e indicata nel suo verso di percorrenza dalla freccia rossa, si perviene al punto 1 sull’asse delle ascisse terminando così l’algoritmo e verificando così graficamente la conferma della Congettura per il numero scelto per questo esempio.
Possiamo osservare anche che perché la Congettura sia verificata non è necessario proseguire graficamente fino a giungere a 1 ma basta raggiungere sull’asse delle ascisse un qualsiasi punto di ascissa pari ad una potenza del 2, infatti per ogni potenza del 2 la Congettura sappiamo che è soddisfatta in quanto l’algoritmo comporta l’applicazione ad essa di una successione di divisioni per 2 un numero di volte pari all’esponente intero positivo di quella potenza fino a giungere proprio ad 1.
Questa dell’approdo nell’algoritmo ad un numero potenza di 2 non è una condizione solo sufficiente per la verifica della Congettura per numeri più grandi di 1, ma anche una condizione necessaria, in quanto almeno si deve passare dal punto di ascissa 2 (quindi la potenza di 2 con esponente 1) per terminare l’algoritmo.
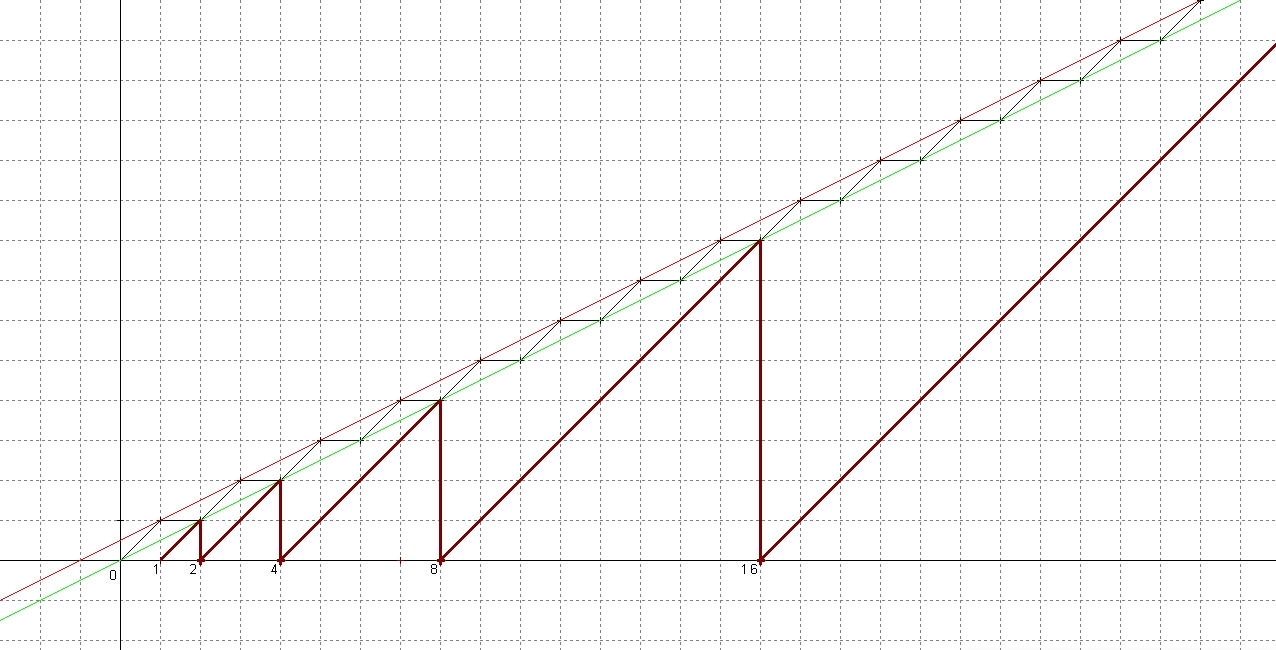
Nella immagine sopra abbiamo rimarcato l’aspetto grafico dell’algoritmo che verifica la Congettura di Collatz per le potenze del 2.
Oreste Caroppo novembre 2023
APPENDICE
Teorema di Caroppo sulla Congettura di Collatz
“Dimostrazione della limitatezza nell’applicazione dell’Algoritmo di Collatz dei possibili tratti crescenti”
Nota: il teorema e le considerazioni qui esposte sono state sviluppate nottetempo tra il 24 e il 25 gennaio 2024 praticamente nel letto durante un incipiente stato influenzale.
Ci vogliamo concentrare qui nell’analisi dei possibili tratti di crescita dell’algoritmo legato alla Congettura di Collatz (che chiameremo qui talvolta Algoritmo di Collatz), pertanto consideriamo la sua applicazione sui numeri dispari
Partiamo da un qualsiasi numero dispari q, esso si potrà sempre scrivere come
q=2n+1 con n numero naturale (includendo anche la possibilità che sia zero),
applicando l’algoritmo abbiamo visto si approda a 3q+1, che essendo però sempre numero pari conduce nell’algoritmo a (3q+1)/2, che possiamo scrivere sostituendo l’espressione di q come (3(2n+1)+1))/2=3n+2
(quando in questa appendice parliamo di applicazione dell’algoritmo della Congettura di Collatz ai dispari sottintenderemo sempre l’insieme dei due passaggi sopra esposti)
Quindi da
2n+1 arrivo a 3n+2
A questo punto ci concentriamo su 3n+1 per il quale non si può sapere a priori, per n generico, se è pari o dispari e valutiamolo a seconda di n, distinguiamo il caso di n pari e quello di n dispari.
Se n pari si potrà scrivere n come n=2m con m numero naturale (includendo anche la possibilità che sia zero), da cui
3(2m)+2=6m+2 che è sempre pari per ogni valore di m, in tal caso termina, per il momento almeno, la crescita tramite l’algoritmo di Collatz.
Se n dispari si potrà scrivere n come n=2m+1 con m numero naturale (includendo anche la possibilità che sia zero), da cui
3(2m+1)+2=6m+5 che è sempre dispari per ogni valore di m
Essendo in tal caso dispari 6m+5 l’Algoritmo di Collatz prevede un passo crescente, rifacendo con 6m+5 i passaggi svolti prima per q otteniamo che da
6m+5 arrivo a 9m+8
A questo punto ci concentriamo su 9m+8 per il quale non si può sapere a priori, per m generico, se è pari o dispari e valutiamolo a seconda di m, distinguiamo il caso di m pari e quello di m dispari.
Se m pari si potrà scrivere n come m=2p con p numero naturale (includendo anche la possibilità che sia zero), da cui
9(2p)+8=18p+8 che è sempre pari per ogni valore di p, in tal caso termina, per il momento almeno, la crescita tramite l’algoritmo di Collatz.
Se m dispari si potrà scrivere m come m=2p+1 con p numero naturale (includendo anche la possibilità che sia zero), da cui
9(2p+1)+8=18p+17 che è sempre dispari per ogni valore di p
Essendo in tal caso dispari 18p+17 l’Algoritmo di Collatz prevede un passo crescente, rifacendo con 18p+17 i passaggi svolti prima per q otteniamo che da
18p+17 arrivo a 27p+26
A questo punto ci concentriamo su 27p+26 per il quale non si può sapere a priori, per p generico, se è pari o dispari e valutiamolo a seconda di p, distinguiamo il caso di p pari e quello di p dispari.
Se p pari si potrà scrivere p come p=2q con q numero naturale (includendo anche la possibilità che sia zero), da cui
27(2q)+26= 54q+26 che è sempre pari per ogni valore di q, in tal caso termina, per il momento almeno, la crescita tramite l’algoritmo di Collatz.
Se p dispari si potrà scrivere p come p=2q+1 con q numero naturale (includendo anche la possibilità che sia zero), da cui
27(2q+1)+26=54q+53 che è sempre dispari per ogni valore di p
Essendo in tal caso dispari 54q+53 l’Algoritmo di Collatz prevede un passo crescente, rifacendo con 54q+53 i passaggi svolti prima per q otteniamo che da
54q+53 arrivo a 81q+80
(…)
Possiamo allora generalizzare ed estrapolare delle formule generiche.
Prima qualche considerazione sui numeri dispari via via considerati.
Consideriamo i numeri naturali
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 …
Di questi soli i numeri naturali dispari
1 – 3 – 5 – 7 – 9 – 11 – 13 – 15 – 17 – 19 – 21 – 23 – 25 – 27 – 29 – 31…
Se li scriviamo come 2n+1 questi che seguono sono gli n corrispondenti a ciascuno di loro
0 -1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10 – 11 – 12 – 13 – 14 – 15…
Di questi n abbiamo considerato solo quelli a loro volta dispari scrivibili come 2m+1 che sono
– -1 – – – 3 – – – 5 – – – 7 – – – 9 – – – 11 – – – 13 – – – 15…
(- -3 – – – 7 – – – 11 – – – 15 – – – 19 – – – 23 – – – 27 – – – 31…
vi corrispondono nella sequenza dei numeri dispari quelli indicati nella seconda fila sopra).
Questi sono gli m corrispondenti a ciascuno di loro
– -0 – – – 1 – – – 2 – – – 3 – – – 4 – – – 5 – – – 6 – – – 7…
Di questi m abbiamo considerato solo quelli a loro volta dispari scrivibili come 2p+1 che sono
– — – – – 1 – – – – – – – 3 – – – – – – – 5 – – – – – – – 7 …
(- — – – – 7 – – – – – – – 15 – – – – – – – 23 – – – – – – – 31…
vi corrispondono nella sequenza dei numeri dispari quelli indicati nella seconda fila sopra).
Questi sono gli p corrispondenti a ciascuno di loro
– — – – – 0 – – – – – – – 1 – – – – – – – 2 – – – – – – – 3 …
Di questi p abbiamo considerato solo quelli a loro volta dispari scrivibili come 2q+1 che sono
– — – – – – – – – – – – – 1 – – – – – – – – – – – – – – – 3 …
(- — – – – – – – – – – – – 15 – – – – – – – – – – – – – – – 31…
vi corrispondono nella sequenza dei numeri dispari quelli indicati nella seconda fila sopra).
e così via.
Ora generalizziamo ed estrapoliamo delle formule generiche.
Se un numero dispari di partenza può essere scritto come
2(… (2(2(2(2(2s+1)+1)+1)+1)+1) …)+1
con s numero naturale includendo la possibilità anche che s sia nullo
con una comparsa ricorsiva per k volte della forma 2n+1 allora esso sarà scrivibile anche come
(2^k)s+1+2+(2^2)+(2^3)+..+2^(k-1)
che possiamo anche riscrivere in maniera più compatta utilizzando la formula per il calcolo della somma di una progressione geometrica di ragione 2 come
(2^k)s+1+2+(2^2)+(2^3)+..+2^(k-1)= (2^k)s+2^(k)-1=(2^k)(s+1)-1
In tal caso l’Algoritmo di Collatz darà una sequenza ininterrotta di crescita in k step fino ad approdare al numero
(3^k)(s)+(3^k)-1=(3^k)(s+1)-1
Per ogni numero dispari, k sarà sempre un numero finito.
Facciamo degli esempi.
Nel caso di 3
3=2(1)+1 k=1 e s=1
Nel caso di 5
5=2(2)+1 k=1 e s=2
Nel caso di 7
7=2(3)+1=2(2(1)+1)+1 k=2 e s=1
Se q=2n+1 ed è esprimibile n=2m+1, m=(n-1)/2<n, quindi ad ogni passaggio abbiamo una diminuzione numerica q<p<m<n,
per cui essendo q finito anche k dovrà essere finito.
Dunque abbiamo ottenuto che tutti i numeri pari o dispari che siano della forma
(3^k)(s)+(3^k)-1
sono punti cui approda l’Algoritmo di Collatz dopo una sequenza di k passaggi tutti crescenti, a partire questi k passaggi finiti dal numero dispari
(2^k)s+1+2+(2^2)+(2^3)+..+2^(k-1)
Se s è pari la sequenza crescente si interrompe.
Se s è dispari la sequenza crescente continuerà oltre.
Nell’ipotesi che si abbia sempre dispari, essendo la sequenza possibile di k passaggi finita, alla fine si avrà s=0
Infatti solo quando s diventa pari a 0 si interrompe la crescita dei dispari nell’algoritmo di Collatz e da lì al successivo si approda ad un numero pari.
L’ultimo numero dispari della serie crescente sarà con s=0
(3^k)-1
per un numero dispari di partenza pari a
1+2+(2^2)+(2^3)+..+2^(k-1)
Ad esempio se parto dal numero dispari 7 nell’Algoritmo di Collatz, al primo passaggio arrivo a 11, k=1
7=2n+1=2*3+1 n=3
n=2*1+1 m=1
m=2*0+1 p=0
al secondo passaggio k=2
approdo a 17
al terzo passaggio k=3
approdo al numero 26 e sono giunto al numero pari
———-
Sappiamo invece che numeri pari del tipo
(2^k)s con s numero naturale
convergono sino a s in k passaggi.
Questi sono due casi estremi di divergenza e convergenza su cui ragionare nello studio della Congettura di Collatz.
———-
Qui anche per dare un senso alle sequenze di numeri sopra esposte osserviamo che un numero dispari, se nell’Algoritmo di Collatz non fa approdare ad un pari, allora sarà un dispari di posizione dispari tra i numeri dispari ordinari in sequenza crescente. Se proseguendo l’algoritmo fa approdare ancora ad un dispari, allora il numero dispari di partenza considerato sarà di posizione dispari tra i numeri dispari già di posizione dispari tra i numeri dispari ordinari in sequenza crescente. E così via eventualmente ma fino ad un numero finito di volte.
Possiamo parlare di numeri dispari di ordine di disparità maggiore. Maggiore è questo ordine di disparità tanto maggiore sarà il k corrispondente, maggior la sequenza crescente di numeri dispari data in loro corrispondenza dall’Algoritmo di Collatz.
k possiamo farlo corrispondere proprio all’ordine di disparità.
Per 7 ad esempio avevamo un k=3 ed in effetti 7 è nella sequenza dei dispari, dove almeno k=1, lo vediamo sopravvissuto nella sequenza dei dispari di posizione dispari per i quali almeno k=2, e infine nella sequenza dei dispari di posizione dispari nella sequenza dei dispari di posizione dispari, per i quali almeno k=3, sparisci infine dalla sequenza ulteriore di posizione dispari in poi.
Abbiamo visto invece come sopravvive il numero dispari 15 nella sequenza successiva in cui era scomparso il 7, per cui 15 ha almeno k=4.
Facciamo degli ultimi esempi di calcolo per il 15
15=2(7)+1=2(2(3)+1)+1=2(2(2(1)+1)3)+1)+1=2(2(2(2(0)+1)+1)3)+1)+1
Per 15 quindi è esattamente k=4
Applicando l’Algoritmo di Collatz arrivo a 80 in 4 step tutti crescenti.
Idem applicando le formule sopra trovate (3^k)-1=3^4-1=80
Interessante allora considerare i numeri dispari
1+2+(2^2)+(2^3)+..+2^(k-1)
1, 3, 7, 15, 31, …
1, 2, 3, 4, 5, …
i k corrispondenti
2, 8, 26, 80, 242, 728, 2186, …
i numeri (3^k)-1 di approdo nella crescita dell’Algoritmo di Collatz in loro corrispondenza
che divisi per 2 danno
1, 4, 13, 40, 121, 364, 1093, …
Ne deduciamo che ((3^k)-1)/2 è dispari per i k dispari
Abbiamo così una stima della massima possibile crescita immediata della sequenza nell’Algoritmo di Collatz per un numero dispari, che non può essere un numero di step volte superiore al k suo proprio o del numero dispari che lo segue della sequenza sopra considerata 1, 3, 7, 15, 31, …
Oreste Caroppo gennaio 2024